Assume that there are x cows and y chickens in the form
Since there are 43 animals, then
Add x and y, then equate the sum by 43
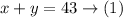
Since a cow has 4 legs and a chicken has 2 legs
Since there are 122 legs, then
Multiply x by 4 and y by 3, then add the products and equate the sum by 122
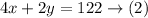
Now, we have a system of equations to solve it
Multiply equation (1) by -2 to make the coefficients of y equal in values and opposite in signs

Add equations (2) and (3) to eliminate y
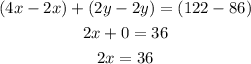
Divide both sides by 2
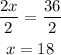
Substitute x by 18 in equation (1)
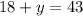
Subtract 18 from each side
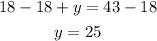
The answer is
There are 18 cows and 25 chickens on the farm