Question

How do I solve this problem?

Answer 1

The probability you're asked to find is


`\mathbb P(A\cup B)-\mathbb P(A\cap B)`

where
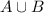
`A\cup B` is the event that either event occurs (A, B, or both), and
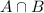
`A\cap B` is the event that both events occur.

Recall that


`\mathbb P(A\cup B)=\mathbb P(A)+\mathbb P(B)-\mathbb P(A\cap B)`

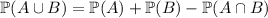
which means


`\mathbb P(A\cup B)-\mathbb P(A\cap B)=\mathbb P(A)+\mathbb P(B)-2\mathbb P(A\cap B)`

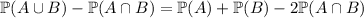
You're told that
`\mathbb P(A)=0.5`,
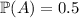
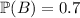
`\mathbb P(B)=0.7`, and (if I'm reading the diagram correctly)
`\mathbb P(A\cap B)=0.3`.

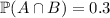
So,


`\mathbb P(A\cup B)-\mathbb P(A\cap B)=0.5+0.7-2*0.3=0.6`

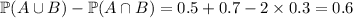
Another way of seeing this is that the event A consists of the regions "A not B" and "A and B". So the probability that "A not B" occurs is


`\mathbb P(A\setminus B)=\mathbb P(A)-\mathbb P(A\cap B)=0.5-0.3=0.2`

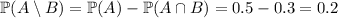
Similarly, B consists of "B not A" and "A and B", so you have


`\mathbb P(B\setminus A)=\mathbb P(B)-\mathbb P(A\cap B)=0.7-0.3=0.4`

So the probability that A or B, but not both, occur is


`\mathbb P(A\setminus B)+\mathbb P(B\setminus A)=0.2+0.4=0.6`