Question

The diameter of a circle is 16 feet. What is the angle measure of an arc bounding a sector with area 8​ square feet?

Answer 1

`45\pi`

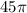
Explanation:

The arc's measure can be found from the sector's area and the circle's area. You already know that the sector's area is 8​ square meters, so find the circle's area.

To find the area, first find the radius.

d

= 2r

16

= 2r Plug in d=16

8

= r Divide both sides by 2

The radius is 8 meters.

Next, find the area of the circle.

A

= ​r2

= ​82 Plug in r=8

= 64​ Square

The area of the circle is 64​ square meters.

Finally, find the angle measure of the arc.

K

= A

m

360

8​

= 64​

m

360

Plug in K=8​ and A=64​

8​

360

64​

= m Multiply both sides by

360

64​

45

= m Multiply and simplify

The angle measure of the arc is 45°.

Answer 2

Diameter is 16 so radius is 8 feet.
Area of the sector is 8 square feet = 1/2*r^2*(angle)
8/ (0.5*8^2)= angle
angle = 0.25