Line equation
Initial explanation
We know that the equation of a line is given by
y = mx + b,
where m and b are numbers: m is its slope (shows its inclination) and b is its y-intercept.
In order to find the equation we must find m and b.
In all cases, m is given, so we must find b.
We use the equation to find b:
y = mx + b,
↓ taking mx to the left side
y - mx = b
We use this equation to find b.
1
We have that the line passes through
(x, y) = (-10, 8)
and m = -1/2
Using this information we replace in the equation we found:
y - mx = b
↓ replacing x = -10, y = 8 and m = -1/2
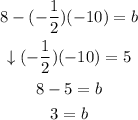
Then, the equation of this line is:
y = mx + b,
↓
y = -1/2x + 3
Equation 1: y = -1/2x + 3
2
Similarly as before, we have that the line passes through
(x, y) = (-1, -10)
and m = 0
we replace in the equation for b,
y - mx = b
↓ replacing x = -1, y = -10 and m = 0
-10 - 0 · (-1) = b
↓ 0 · (-1) = 0
-10 - 0 = b
-10 = b
Then, the equation of this line is:
y = mx + b,
↓
y = 0x - 10
y = -10
Equation 2: y = -10
3
Similarly as before, we have that the line passes through
(x, y) = (-6, -9)
and m = 7/6
we replace in the equation for b,
y - mx = b
↓ replacing x = -6, y = -9 and m = 7/6
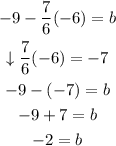
Then, the equation of this line is:
y = mx + b,
↓
y = 7/6x - 2
Equation 3: y = 7/6x - 2
4
The line passes through
(x, y) = (6, -4)
and m = does not exist
When m does not exist it means that the line is vertical, and the equation looks like:
x = c
In this case
(x, y) = (6, -4)
then x = 6
Then
Equation 4: x = 6
5
The line passes through
(x, y) = (6, -6)
and m = 1/6
we replace in the equation for b,
y - mx = b
↓ replacing x = 6, y = -6 and m = 1/6

Then, the equation of this line is:
y = mx + b,
↓
y = 1/6x - 7
Equation 5: y = 1/6x - 7