
The rows add up to
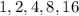
, respectively. (Notice they're all powers of 2)
The sum of the numbers in row

is

.
The last problem can be solved with the binomial theorem, but I'll assume you don't take that for granted. You can prove this claim by induction. When
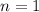
,
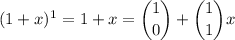
so the base case holds. Assume the claim holds for
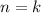
, so that
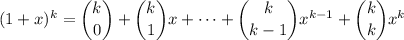
Use this to show that it holds for
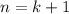
.
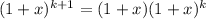
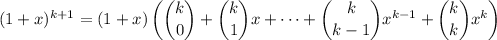

Notice that

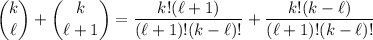
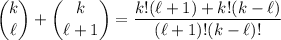
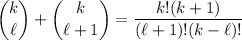
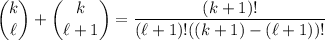
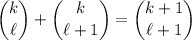
So you can write the expansion for
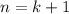
as
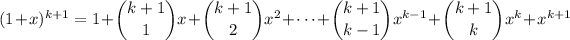
and since
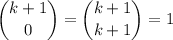
, you have
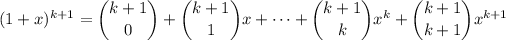
and so the claim holds for
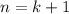
, thus proving the claim overall that

Setting
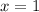
gives
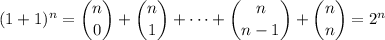
which agrees with the result obtained for part (c).