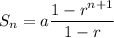Let
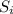
denote the

th partial sum of a geometric sequence with common ratio

. The sum of the first

terms of the sequence is
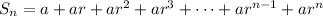
.
Suppose we multiply both sides by

, then
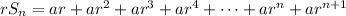
Taking the difference makes most of the terms vanish:

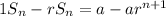
Then solving for

gives the formula.