Answer:
Option b.
Explanation:
Given information :

We need to check which congruence statement does not necessarily describe the triangles shown if
 .
.
Corresponding part of congruent triangles are congruent.
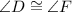


Using these corresponding angles we can say that




In the given options
 ,
,
 and
and
 congruence statement are true.
congruence statement are true.
Only
 does not necessarily describe the triangles.
does not necessarily describe the triangles.
Therefore, the correct option is b.