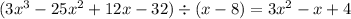Question

Drag the numbers to the correct locations on the image. Not all numbers will be used.

Complete the synthetic division to find the quotient of and .

Answer 1

`\frac{(3 {x}^(3) - 25 {x}^(2) + 12x - 32)}{(x - 8)} = (3 {x}^(2) - x + 4)\\`

Answer 2

First Column: 8

Third Column: 24

Fourth Column: 4

Fifth Column (from top to bottom): 32; 0

This means that:

`(3x^3-25x^2+12x-32)/ (x-8)=3x^2-x+4`

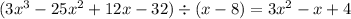
Explanation:

We can perform synthetic division when we divide a polynomial P(x) by a binomial in the form of (x - a).

When doing so, the number that goes to the very left of our structure will be the constant a.

We fill the first row with the coefficients of each term.

We are dividing
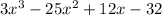`3x^3-25x^2+12x-32` by
`x-8`.

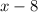So, a = 8.

Therefore, for the first column, the number there is 8.

The second column has been filled out.

For the third column, we multiply the previous number by our a.

The previous number is 3. 3(8) is 24.

So, the number in the third column is 24.

(And we add 24 to -25 to acquire -1).

So, for the fourth column, we will add the two numbers to acquire (12 - 8) = 4.

Hence, the number for the fourth column is 4.

For the fifth column, the top box, it will again be the previous number multiplied by our a.

The previous number is 4. 4(8) is 32.

So, the number in the top box of the fifth column is 32.

And when added to -32, it equates to 0. Hence, the second box of the fifth column is 0.

This means that:

`(3x^3-25x^2+12x-32)/ (x-8)=3x^2-x+4`