Question

the mean salary offered to students who are graduating from coastal state university this year is $24,215, with a standard deviation of $3712. A random sample of 80 coastal state students graduating this year has been selected. What is the probability that the mean salary offer for these 80 students is $24,250 or more?

Answer 1

Given that the mean and standard deviation of the population are $24,215 and $3712 respectively,

`\begin{gathered} \mu=24215 \\ \sigma=3712 \end{gathered}`

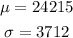
The sample size taken is 80,

`n=80`

Consider that the salary of students in the sample is assumed to follow Normal Distribution with mean and standard deviation as follows,

`\begin{gathered} \mu_x=\mu\Rightarrow\mu_x=24215 \\ \sigma_x=\frac{\sigma}{\sqrt[]{n}}=\frac{3712}{\sqrt[]{80}}\approx415 \end{gathered}`

So the probability that the mean salary (X) is $24250 or more, is calculated as,

So the approximate value for z=0.084 is,

`\emptyset(0.084)=(0.0319+0.0359)/(2)=0.0339`

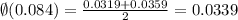
Substitute the value in the expression,

`\begin{gathered} P(X\ge24250)=0.5-0.0339 \\ P(X\ge24250)=0.4661 \end{gathered}`

Thus, there is a 0.4661 probability that the mean salary offer for these 80 students is $24,250 or more.