Question

The center of mass of a cow and the center of mass of a tractor are 208 meters apart. The magnitude of the gravitational force of attraction between these two objects is calculated to be 1.8 × 10-9 newtons.

What would the magnitude of the gravitational force of attraction be between these two objects if they were 416 meters apart?
A.
1.62 × 10-9 newtons
B.
3.6 × 10-10 newtons
C.
9 × 10-10 newtons
D.
4.5 × 10-10 newtons

Answer 1

Choice: D.

Step-by-step explanation:

Newton’s Law of Universal Gravitation

It states that objects attract each other with a force that is proportional to their masses and inversely proportional to the square of the distance between them. The formula is:

`\displaystyle F=G{\frac {m_(1)m_(2)}{r^(2)}}`

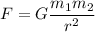
Where:

m1 = mass of object 1

m2 = mass of object 2

r = distance between the objects' center of masses

G = gravitational constant:
`6.67\cdot 10^(-11)~Nw*m^2/Kg^2`

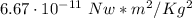
The center of mass of a cow is at a distance of r=208 m from the center of the mass of a tractor. The gravitational force of attraction is
`F=1.8\cdot 10^(-9)\ N`. It's required to find the new force of attraction F' if the distance was r'=416 m.

It can be noted that r'=2r. If the distance is doubled, the new force is:

`\displaystyle F'=G{\frac {m_(1)m_(2)}{(2r)^(2)}}`

`\displaystyle F'=(1)/(4)G{\frac {m_(1)m_(2)}{r^(2)}}`

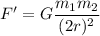
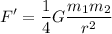
Substituting the original value of F:

`\displaystyle F'=(1)/(4)\cdot 1.8\cdot 10^(-9)\ N`

Operating:

`\displaystyle F'=4.5\cdot 10^(-10)\ N`

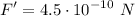
Choice: D.