Question

A ball with a mass of 0.8 kg is thrown straight upward, flies up to its maximum height, and

then falls back down. If the ball reaches a maximum height of 10.7 meters, how fast was the
ball thrown initially? Round your answer to the tenths place.

Answer 1

v = 14.5 m/s

Step-by-step explanation:

The Principle Of Conservation Of Mechanical Energy

In the absence of friction, the total mechanical energy is conserved. That means that

Em=U+K is constant, being U the potential energy and K the kinetic energy

U=mgh

`\displaystyle K=(mv^2)/(2)`

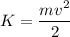
The ball with a mass of m=0.8 kg is thrown straight upward from the zero height reference (h=0) and with some speed (v). The potential energy is zero, but the kinetic speed is given by the equation above.

When the ball reaches its maximum height of h=10.7 m, the speed is zero and all the initial kinetic energy was transformed into potential energy, thus:

`\displaystyle (mv^2)/(2)=mgh`

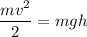
Simplifying by m:

`\displaystyle (v^2)/(2)=gh`

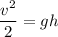
Solving for v:

`\displaystyle v=√(2gh)`

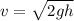
Substituting:

`\displaystyle v=√(2*9.8*10.7)`

Calculating:

v = 14.5 m/s