Question

I only need part bb) A foam protector is covered with PVC material to make it waterproof. Find the total surface area of a protector which is covered by PVCmaterial.

Answer 1

Assuming all the parts are covered, inluding the internal part, we have to find the surface area of the whole protector.

So, let's list which areas we need:

- We need the lateral areas of the external parts, which are 4 rectangles.

- We need the top and bottom areas, which are both area of squares minus the area of the cicle of the hole.

- We need the interior aread, which is the same as the lateral area of a cylinder.

For the external part, we only need the dimensions of each rectangle. since they have the same length and the other sides are the sides of the squares, they are all the same.

The area of each of them is:

`A_{\text{rectangle}}=300mm\cdot1.8m=0.3m\cdot1.8m=0.54m^2`

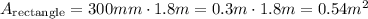
Since we have 4, the total exterior lateral area is:

`A_{\text{lateral}}=4\cdot0.54m^2=2.16m^2`

For the top and bottom, both are the same, a square of 300 mm x 300 mm with a hole of 150 mm diameter.

First, let's get all to meters: 0.3 m x 0.3 m and 0.15 m diameter. The radius of the circle is half the diameter, so:

`r=(0.15m)/(2)=0.075m`

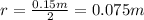
The area of a circle given its radius is:

`A=\pi r^2`

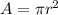
So, the area of both the top and bottom is the area of the square minus the area of the circle and double all of this:

`\begin{gathered} A_{\text{top/ottom}}=2((0.3m)^2-\pi(0.075m)^2) \\ A_{\text{top/ottom}}=2(0.09m^2-0.005625\pi m^2) \\ A_{\text{top/ottom}}=2(0.09-0.005625\pi)m^2 \end{gathered}`

We deal with π later on.

For the lateral area of the cylinder, we can remember that it is the same as the area of a rectangle with on dimension being the length of the cylinder and the other being the circumference of the top/bottom.

the circumference of a circle is:

`C=2\pi r`

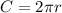
The radius is the same as the hole, and the length is 1.8m, so the lateral area of the cylinder is:

`\begin{gathered} A_{\text{cylinder}}=1.8m\cdot2\pi(0.075m) \\ A_{\text{cylinder}}=(1.8\cdot0.15\pi)m^2 \\ A_{\text{cylinder}}=(0.27\pi)m^2 \end{gathered}`

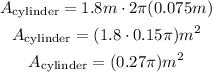
So, the total surface area is the sum of all of these:

`A=2.16m^2+2(0.09-0.005625\pi)m^2+(0.27\pi)m^2`

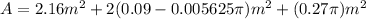
Now, we just need to evaluate:

`\begin{gathered} A=2.16m^2+2\cdot0.072328\ldots m^2+0.848230\ldots m^2 \\ A=2.16m^2+0.144657\ldots m^2+0.848230\ldots m^2 \\ A=3.152887\ldots m^2 \\ A\approx3.15m^2 \end{gathered}`

So, the lateral area is approximately 3.15 m².