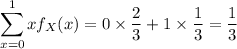Question

A computer program contains one error. In order to find the error, we split the program into 6 blocks and test two of them, selected at random. Let X be the number of errors in these blocks. Compute E(X).

Answer 1

There are
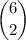
`\dbinom62` ways of selecting two of the six blocks at random. The probability that one of them contains an error is


`(\dbinom11\dbinom51)/(\dbinom62)=\frac5{15}=\frac13`

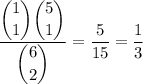
So
`X` has probability mass function


`f_X(x)=\begin{cases}\frac13&\text{for }x=1\\\\\frac23&\text{for }x=0\end{cases}`

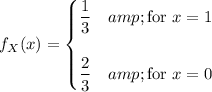
These are the only two cases since there is only one error known to exist in the code; any two blocks of code chosen at random must either contain the error or not.

The expected value of finding an error is then


`\displaystyle\sum_(x=0)^1xf_X(x)=0*\frac23+1*\frac13=\frac13`