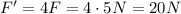Answer:
20 N
Step-by-step explanation:
The gravitational force between the two objects is given by:
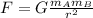
where
G is the gravitational constant
mA and mB are the masses of the two objects
r is the separation between the two objects
In this situation, we have that the distance between the two objects is reduced in half. Let's call the new distance
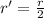
So the new gravitational force F' will be
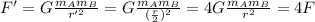
So, the force increases by a factor 4, therefore the new force will be