Answer:
The volume of the resulting solid is eight times smaller than the volume of the original solid
Explanation:
we know that
If two figures are similar, then the ratio of its volumes is equal to the scale factor elevated to the cube
Let
z-----> the scale factor
x------> the volume of the resulting solid
y-----> the volume of the original solid
so
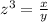
In this problem we have
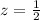
substitute
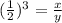
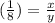
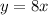
The volume of of the original solid is eight times larger than the volume of the resulting solid
or
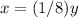
The volume of the resulting solid is eight times smaller than the volume of the original solid