Question

Jessie received the following scores on her math tests this year. (45, 65, 70, 80, 85, 100) Suppose the teacher removes the lowest and highest scores. (65, 70, 80, 85) What are the interquartile ranges of Jessie’s original scores and her new scores?

Answer 1

original :
(45,65,70,80,85,100)
Q1 = 65
Q2 = (70 + 80) / 2 = 150/2 = 75
Q3 = 85
IQR = Q3 - Q1 = 85 - 65 = 20

new :
(65,70,80,85)
Q1 = (65 + 70)/2 = 135/2 = 67.5
Q2 = (70 + 80) / 2 = 75
Q3 = (80 + 85) / 2 = 165/2 = 82.5
IQR = Q3 - Q1 = 82.5 - 67.5 = 15

IQR of original = 20 <=====
IQR of new = 15 <=====

Answer 2

interquartile range of original data:20

New data:15

Explanation:

The original data is given as:

45 65 70 80 85 100.

lower quartile(
`Q_(1)`)=65

median of data(
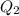`Q_(2)`)=(70+80)/2=75

upper quartile(
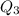`Q_(3)`)=85

interquartile range=
`Q_(3)`-
`Q_(1)`

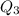=85-65=20

The changed data is given as:

65 70 80 85

lower quartile(
`Q_(1)`)=(65+70)/2=67.5

median(
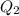`Q_(2)`)=(70+80)/2=75

upper quartile(
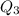`Q_(3)`)=(80+85)/2=82.5

interquartile range=
`Q_(3)`-
`Q_(1)`

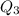=82.5-67.5=15.