Question

Solve triangle ABC. (If an answer does not exist, enter DNE. Round your answers to one decimal place.) a = 3.0, b = 4.0, C = 58°

Answer 1

A = 46.3°

B = 75.7°

c = 3.5

Step-by-step explanation

We will be using both Cosine and Sine rule to solve this.

For Cosine rule,

If a triangle ABC has angles A, B and C at the points of the named vertices of the tringles with the sides facing each of these angles tagged a, b and c respectively, the Cosine rule is given as

c² = a² + b² - 2ab Cos C

a = 3.0

b = 4.0

C = 58°

c² = 3² + 4² - 2(3)(4)(Cos 58°)

c² = 9 + 16 - (24)(0.5299)

c² = 25 - 12.72 = 12.28

c = √12.28 = 3.50

To find the other angles, we will now use Sine Rule

If a triangle ABC has angles A, B and C at the points of the named vertices of the tringles with the sides facing each of these angles tagged a, b and c respectively, the sine rule is given as

`\frac{\text{ Sin A}}{a}=\frac{\text{ Sin B}}{b}=\frac{\text{ Sin C}}{c}`

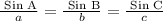
So, we can use the latter parts to solve this

`\frac{\text{ Sin B}}{b}=\frac{\text{ Sin C}}{c}`

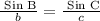
B = ?

b = 4.0

C = 58°

c = 3.5

`\begin{gathered} \frac{\text{ Sin B}}{4}=\frac{\text{ Sin 58}\degree}{3.5} \\ \text{ Sin B = }\frac{4*\text{ Sin 58}\degree}{3.5}=0.9692 \\ B=Sin^(-1)(0.9692)=75.7\degree \end{gathered}`

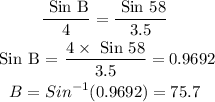
We can then solve for Angle A

The sum of angles in a triangle is 180°

A + B + C = 180°

A + 75.7° + 58° = 180°

A = 180° - 133.7° = 46.3°

Hope this Helps!!!