Question

The interior angles of a hexegon are in the ratio 3:3:4:5:6:7. Find; (a) The size of the smallest angle. (b) The size of the largest angle​

Answer 1

Answer: (a)
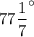`77\frac17^(\circ)` (b) 180°

Step-by-step explanation:

Sum of interior angles of a polygon with n-sides:
`(n-2)*180^(\circ)`

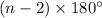
In hexagon, total sides: n =6

Given: The interior angles of a hexagon are in the ratio 3:3:4:5:6:7.

Let the angles be 3x , 3x, 4x, 5x, 6x, 7x

Then,

`3x+3x+4x+5x+6x+7x=(6-2)*180^(\circ)\\\\\Rightarrow\ 28x=4* 180\\\\\\\Rightarrow\ x=(4*180)/(28)\\\\\Rightarrow\ x=25(5)/(7)^(\circ)`

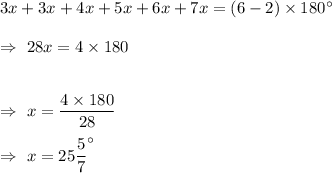
Smallest angle= 3x =
`3* (180)/(7)=77\frac17^(\circ)`

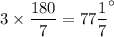
Largest angle = 7x =
`7*(180)/(7)=180^(\circ)`