Question

A scientist has discovered an organism that produces five offspring exactly one hour after its own birth, and then goes on to live for one week. Each replicated organism also replicates at the same rate. At hour one, there is one organism. At hour two, there are five more organisms. How many total organisms are there at hour seven?

Answer 1

After 7 hours number of organisms would be 19531

Solution-

At hour one, there is one organism. At hour two, there are five more organisms.

So the number of organism in each hour would be,

1, 5, 25, 125,......... so on

This series is in Geometrical Progression.

Sum of first n terms of a G.P.

`S_n=(a(r^n-1))/(r-1)`

where,

a = first term = 1

r = common ratio = 5

n = 7

Putting the values,

`S=(1(5^7-1))/(5-1)`

`=(5^7-1)/(4)`

`=(78125-1)/(4)`

`=(78124)/(4)`

`=19531`

Therefore, after 7 hours number of organisms would be 19531

Answer 2

At hour one, there is 1 organism.

At hour two, there are 5 more organisms.

At hour three, there are 25 more organisms.

At hour four, there are 125 more organisms.

At hour five, there are 625 more organisms.

At hour six, there are 3125 more organisms.

At hour seven, there are 15625 more organisms.

In total, there are 1+5+25+125+625+3125+15625=19531 organisms.

Answer: 19531 organisms.

Another way: this is the geometrical sequence with

`a_1=1,\\ r=5,\\S_7-?`

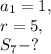
Use formula
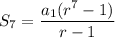`S_7=(a_1(r^7-1))/(r-1)` to count how many total organisms are there at hour seven. Thus,

`S_7=(1\cdot (5^7-1))/(5-1)=(78124)/(4)=19531.`

This way is strong mathematical way))