Question

Hello! Need a little help on parts a,b, and c. The rubric is attached, Thank you!

Answer 1

In this situation, The number of lionfish every year grows by 69%. This means that to the number of lionfish in a year, we need to add the 69% to get the number of fish in the next year.

This is a geometric sequence because the next term of the sequence is obtained by multiplying the previous term by a number.

The explicit formula for a geometric sequence is:

`a_n=a_1\cdot r^(n-1)`

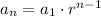
We know that a₁ = 9000 (the number of fish after 1 year)

And the growth rate is 69%, to get the number of lionfish in the next year, we need to multiply by the rate og growth (in decimal) and add to the number of fish. First, let's find the growth rate in decimal, we need to divide by 100:

`(69)/(100)=0.69`

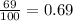
Then, if a₁ is the number of lionfish in the year 1, to find the number in the next year:

`a_2=a_1+a_1\cdot0.69`

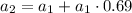
We can rewrite:

`a_2=a_1(1+0.69)=a_1(1.69)`

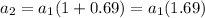
With this, we have found the number r = 1.69. And now we can write the equation asked in A:

The answer to A is:

`f(n)=9000\cdot1.69^(n-1)`

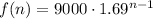
Now, to solve B, we need to find the number of lionfish in the bay after 6 years. Then, we can use the equation of item A and evaluate for n = 6:

`f(6)=9000\cdot1.69^(6-1)=9000\cdot1.69^5\approx124072.6427`

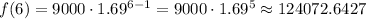
To the nearest whole, the number of lionfish after 6 years is 124,072.

For part C, we need to use the recursive form of a geometric sequence:

`a_n=r(a_(n-1))`

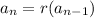
We know that the first term of the sequence is 9000. After the first year, the scientists remove 1400 lionfish. We can write this as:

`\begin{gathered} a_1=9000 \\ a_n=r\cdot(a_(n-1)-1400) \end{gathered}`

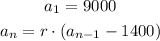
Because to the number of lionfish in the previous year, we need to subtract the 1400 fish removed by the scientists.

The answer to B is: