Question

The glide slope is the path a plane uses while it is landing on a runway. The glide slope usually makes a 3º angle with the ground. A plane is on the glide slope and is 1 mile (5280 feet) from touchdown. Use the tangent ratio and a calculator to find EF (the altitude of the plane) to the nearest foot. The plane is ____ feet high. (Enter only the number.)

Answer 1

the altitude of the plane to the nearest foot is, 277 feet high

Explanation:

Using tangent ratio:

`\tan \theta = \frac{\text{Opposite side}}{\text{Adjacent side}}`

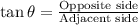
As per the statement:

The glide slope usually makes a 3º angle with the ground.

⇒
`\theta = 3^(\circ)`

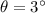
A plane is on the glide slope and is 1 mile (5280 feet) from touchdown.

⇒Adjacent side= DF = 1 mi = 5280 feet.

We have to find the EF.

Using tangent ratio:

`\tan \theta^(\circ)= \frac{\text{EF}}{\text{DF}}`

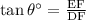
Substitute the given values we have;

`\tan 3^(\circ)= \frac{\text{EF}}{5280}`

Multiply both sides by 5280 we have;

`\text{EF} = 5280 \cdot \tan 3^(\circ)`

⇒
`\text{EF} = 5280 \cdot 0.05240777928`

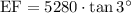
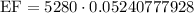
Simplify:

EF = 276.713074614 feet.

Therefore, the altitude of the plane to the nearest foot is, 277 feet high

Answer 2

tan∅ = height / base
height = tan(3) x 5280
height = 276.7 feet