Question

Find the length of DE. Round to the nearest hundredth. (Picture included)

Answer 1

notice the picture
we have, the opposite side
the angle
and we want the hypotenuse

so recall your SOH CAH TOA
`\bf sin(\theta)=\cfrac{opposite}{hypotenuse} \qquad \qquad % cosine cos(\theta)=\cfrac{adjacent}{hypotenuse} \\ \quad \\\\ % tangent tan(\theta)=\cfrac{opposite}{adjacent} =`

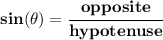
which one has all that? low and behold, is Ms Sine,
so let's bother Ms Sine


`\bf sin(\theta)=\cfrac{opposite}{hypotenuse}\implies sin(27^o)=\cfrac{18}{hypotenuse} \\\\\\ hypotenuse=\cfrac{18}{sin(27^o)}`

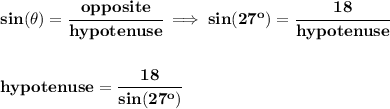
make sure your calculator is in Degree mode, since the angle here is in degrees, as opposed to Radian mode

Answer 2

Based on the right-angled triangle shown above, the length of segment DE is equal to 39.65 units.

In order to determine the length of segment DE, we would apply the basic sine trigonometric ratio because the given side lengths represent the opposite side (DC) and hypotenuse (DE) of a right-angled triangle;

sin(θ) = Opp/Hyp

Where:

• Opp represent the opposite side of a right-angled triangle.
• Hyp represent the hypotenuse of a right-angled triangle.
• θ represent the angle.

Based on right-angled triangle CDE, an equation for the sine trigonometric ratio is as follows;

sin(θ) = Opp/Hyp

sin(27) = DC/DE

sin(27) = 18/DE

DE = 18/sin(27)

DE = 39.6484 ≈ 39.65 units.