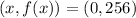Question

Use the second derivative test to classify the relative extrema if the test applies

Answer 1

The answer is:

`(x,f(x))=(0,256)`

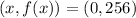
SOLUTION

Problem Statement

The question gives us a polynomial expression and we are asked to find the relative maxima using the second derivative test.

The function given is:

`(3x^2+16)^2`

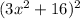
Method

To find the relative maxima, there are some steps to perform.

1. Find the first derivative of the function

2. Equate the first derivative to zero and solve for x.

3. Find the second derivative of the function.

4. Apply the second derivative test:

This test says:

`\begin{gathered} \text{ If }a\text{ is one of the roots of the equation from the first derivative, then,} \\ f^(\doubleprime)(a)>0\to\text{There is a relative minimum} \\ f^(\doubleprime)(a)<0\to\text{There is a relative maximum} \end{gathered}`

5. Find the Relative Minimum

Implementation

1. Find the first derivative of the function

`\begin{gathered} f(x)=(3x^2+16)^2 \\ \text{Taking the first derivative of both sides, we have:} \\ f^(\prime)(x)=6x*2(3x^2+16) \\ f^(\prime)(x)=12x(3x^2+16) \end{gathered}`

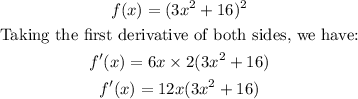
2. Equate the first derivative to zero and solve for x.

`\begin{gathered} f^(\prime)(x)=12x(3x^2+16)=0 \\ \text{This implies that,} \\ 12x=0\text{ OR }3x^2+16=0 \\ \therefore x=0\text{ ONLY} \\ \\ \text{Because }3x^2+16=0\text{ has NO REAL Solutions} \end{gathered}`

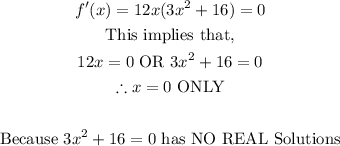
This implies that there is ONLY ONE turning point/stationary point at x = 0

3. Find the second derivative of the function:

`\begin{gathered} f^(\prime)(x)=12x(3x^2+16) \\ f^(\doubleprime)(x)=12(3x^2+16)+12x(6x) \\ f^(\doubleprime)(x)=36x^2+192+72x^2 \\ \therefore f^(\doubleprime)(x)=108x^2+192 \end{gathered}`

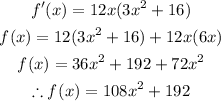
4. Apply the second derivative test:

`\begin{gathered} f^(\doubleprime)(x)=108x^2+192 \\ a=0,\text{ which is the root of the first derivative }f^(\prime)(x) \\ f^(\doubleprime)(a)=f^(\doubleprime)(0)=108(0)^2+192 \\ f^(\doubleprime)(0)=192>0 \\ \\ By\text{ the second derivative test,} \\ f^(\doubleprime)(0)>0,\text{ thus, there exists a relative minimum at }x=0\text{ } \\ \\ \text{ Thus, we can find the relative minimum when we substitute }x=0\text{ into the function }f(x) \end{gathered}`

5. Find the Relative Minimum:

`\begin{gathered} f(x)=(3x^2+16)^2 \\ \text{substitute }x=0\text{ into the function} \\ f(0)=(3(0)^2+16)^2 \\ f(0)=16^2=256 \\ \\ \text{Thus, the minimum value of the function }f(x)\text{ is }256 \\ \\ \text{The coordinate for the relative minimum for the function }(3x^2+16)^2\text{ is:} \\ \mleft(x,f\mleft(x\mright)\mright)=\mleft(0,f\mleft(0\mright)\mright) \\ \text{But }f(0)=256 \\ \\ \therefore(x,f(x))=(0,256) \end{gathered}`

Since the function has ONLY ONE turning point, and the turning point is a minimum value, then THERE EXISTS NO MAXIMUM VALUE

Final Answer

The answer is:

`(x,f(x))=(0,256)`