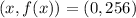Answer
The answer is:
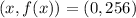
SOLUTION
Problem Statement
The question gives us a polynomial expression and we are asked to find the relative maxima using the second derivative test.
The function given is:
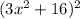
Method
To find the relative maxima, there are some steps to perform.
1. Find the first derivative of the function
2. Equate the first derivative to zero and solve for x.
3. Find the second derivative of the function.
4. Apply the second derivative test:
This test says:

5. Find the Relative Minimum
Implementation
1. Find the first derivative of the function
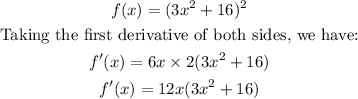
2. Equate the first derivative to zero and solve for x.
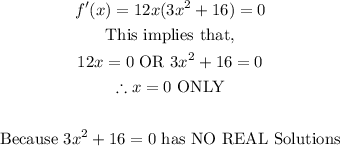
This implies that there is ONLY ONE turning point/stationary point at x = 0
3. Find the second derivative of the function:
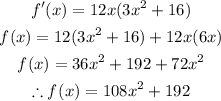
4. Apply the second derivative test:

5. Find the Relative Minimum:

Since the function has ONLY ONE turning point, and the turning point is a minimum value, then THERE EXISTS NO MAXIMUM VALUE
Final Answer
The answer is: