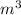Question

A prism with a base area of 3 m² and a height of 4 m is dilated by a factor of 3/2 . What is the volume of the dilated prism?

Answer 1

Volume of Original Prism = base area * Height = 3 * 4 = 12

After dilation factor = 12 * 3/2 = 6 * 3 = 18

In short, Your Answer would be 18 m³

Hope this helps!

Answer 2

Scale factor(k)defined as the ratio of image to the pre-image i,e

`k = \frac{\text{Image}}{\text{Pre-image}}`

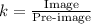
Volume of a prism is given by:

`V = A \cdot h`

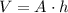
where

V is the volume of the prism

A is the base Area

h is the height.

As per the statement:

A prism with a base area of 3 m² and a height of 4 m

⇒Base area(A) = 3 m² and height(h) = 4 m

Then by definition of volume of prism

Volume of the original prism =
`3 \cdot 4 = 12 m^3`

Since, the prism is dilated by a factor of 3/2

⇒
`k = (3)/(2)`

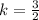
then by definition of scale factor:

`k= \frac{\text{Dilated volume of prism}}{\text{Original prism}}`

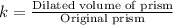
Substitute the given values we have;

`(3)/(2) = \frac{\text{Dilated Volume of prism}}{12}`

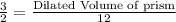
Multiply both sides by 12 we have;

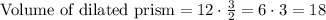`\text{Volume of dilated prism} = 12 \cdot (3)/(2) = 6 \cdot 3 = 18` cubic meter

Therefore, the volume of dilated prism is, 18
`m^3`