Question

Solve this equation for x in terms of t using cramer's rule: (t)x+(2t+1)y=(t+1)

(t-1)x+(2t)y=t(t+1)

Answer 1

`tx+(2t+1)y=t+1\\ (t-1)x+(2t)y=t(t+1)`

So our coefficient matrix is given by:

`\left[\begin{array}{cc}t&(2t+1)\\ (t-1)& 2t\end{array}\right]`

Taking the determinant of our coefficient matrix:

`D=\left|\begin{array}{cc}t&(2t+1)\\ (t-1)& 2t\end{array}\right|=t(2t)-(2t+1)(t-1)=t+1`

If we take the determinant of our coefficient matrix with x-column replaced by the answer column values:

`D_x= \left|\begin{array}{cc}(t+1)&(2t+1)\\ t(t+1)& 2t\end{array}\right|=(t+1)(2t)-(2t+1)t(t+1)\\ \\ D_x=-2t^3-t^2+t`

Cramer's Rule tells us:

`x=(D_x)/(D)=(-2t^3-t^2+t)/(t+1)`

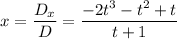
Applying Polynomial Long Division or Synthetic Division (with -1) should give you the result -2t^2+t if I did my calculations correctly.

This can be factored, giving us a nicer looking answer of
`x=t(1-2t)`

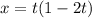
This is a fairly long problem, easy to get confused along the way. Lemme know if anything didn't make sense.