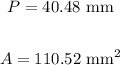Question

#2 Funding the perimeter and area of the composite figure.

Answer 1

1)

We can find the circumference using the formula

`C=2\pi r`

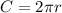
but remember that the diameter is 2 times the radius

`d=2r`

So we can use the formula using radius or diameter, the problem gives us the diameter, so let's use it, so the formula will change a little bit

`C=\pi d`

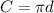
Where "d" is the diameter.

d = 40 yd, and π = 3.14, so the circumference will be

`\begin{gathered} C=\pi d \\ C=3.14\cdot40=125.6\text{ yd} \end{gathered}`

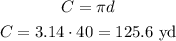
And to find out the area we can use this formula

`A=(\pi d^2)/(4)`

Or if you prefer use the radius

`A=\pi r^2`

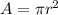
Let's use the formula with the diameter again

`\begin{gathered} A=(\pi d^2)/(4) \\ \\ A=(3.14\cdot(40)^2)/(4) \\ \\ A=1256\text{ yd}^2 \end{gathered}`

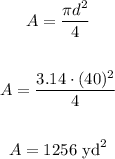
Then the circumference is 125.6 yd and the area is 1256 yd^2

2)

Here we have a compounded figure, we have half of a circle and a triangle, so let's think about how we get the perimeter and the area.

The perimeter will be the sum of the sides of the triangle and half of a circumference, we already know the length of the triangle's side, it's 10.82, we got to find the half of a circle circumference and then sum with the sides.

We know that

`C=\pi d`

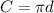
And we can see in the figure that d = 12 mm, then

`C=\pi d=3.14\cdot12=37.68\text{ mm}`

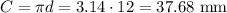
But that's a full circumference, we just want half of it, so let's divide it by 2.

`(C)/(2)=(37.68)/(2)=18.84\text{ mm}`

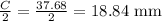
Now we have half of a circumference we can approximate the perimeter of the figure, it will be

`\begin{gathered} P=10.82+10.82+18.84 \\ \\ P=40.48\text{ mm} \end{gathered}`

The area will be the area of the triangle sum the area of half of a circle

Then let's find the triangle's area first

`A_{}=(b\cdot h)/(2)`

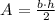
The base "b" will be the diameter of the circle, and the height "h" will be 9 mm, then

`A_{}=(12\cdot9)/(2)=54\text{ mm}^2`

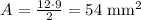
And the half of a circle's area will be

`A=(1)/(2)\cdot(\pi d^2)/(4)=(3.14\cdot(12)^2)/(8)=$$56.52$$\text{ mm}^2`

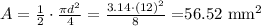
Then the total area will be

`A_T=56.52+54=110.52\text{ mm}^2`

Therefore, the perimeter and the area is

`\begin{gathered} P=40.48\text{ mm} \\ \\ A=110.52\text{ mm}^2 \end{gathered}`