Question

The center of mass of a cow and the center of mass of a tractor are 208 meters apart. The magnitude of the gravitational force of attraction between these two objects is calculated to be 1.8 × 10-9 newtons.

What would the magnitude of the gravitational force of attraction be between these two objects if they were 416 meters apart?
A.
1.62 × 10-9 newtons
B.
3.6 × 10-10 newtons
C.
9 × 10-10 newtons
D.
4.5 × 10-10 newtons

Answer 1

The magnitude of the gravitational force of attraction between the two objects when they are 416 meters apart is;

D. 4.5 × 10⁻¹⁰ Newtons

Step-by-step explanation:

The given parameters are;

The distance between the center of mass of the cow and the tractor, r = 208 m

The gravitational attraction between the cow and the tractor = 1.8 × 10⁻⁹ N

The formula for finding the gravitational force, 'F', between the cow and the tractor is given as follows;

`F =G\cdot (m_(1) \cdot m_(2))/(r^(2))`

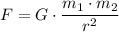
Where;

G = The universal gravitational constant = 6.67408 × 10⁻¹¹m³·kg⁻¹·s⁻²

m₁·m₂ = The product of the mass of the cow and the tractor

Therefore, we have;

`F = 1.8 * 10^(-9) =G\cdot (m_(1) \cdot m_(2))/(208^(2))`

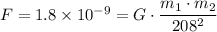
1.8 × 10⁻⁹ × 208² ≈ 7.78752 × 10⁻⁵ = G × m₁ × m₂

Therefore, when the distance between the two objects are 416 meters apart, we have;

`F = (G \cdot m_(1) \cdot m_(2))/(r^(2)) = (7.78752 * 10^(-5))/(416^2) = 4.5 * 10^(-10)`

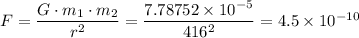
The magnitude of the gravitational force of attraction between the cow and the tractor when they are 416 meters apart, F = 4.5 × 10⁻¹⁰ N.