Question

Two containers designed to hold water are side by side, both in the shape of acylinder. Container A has a diameter of 8 feet and a height bf 16 feet. Container B hasa diameter of 10 feet and a height of 8 feet. Container A is full of water and the wateris pumped into Container B until Conainter B is completely full.To the nearest tenth, what is the percent of Container A that is empty after thepumping is complete?

Answer 1

Okay, here we have this:

Considering the provided information, we are going to calculate what is the percent of Container A that is empty after the pumping is complete, so we obtain the following:

First we will calculate the volume of each cylinder using the following formula:

`V=\pi\cdot r^2\cdot h`

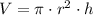
Applying:

`\begin{gathered} V_A=\pi\cdot4^2\cdot16 \\ V_A=\pi\cdot16\cdot16 \\ V_A=256\pi \end{gathered}`
`\begin{gathered} V_B=\pi\cdot5^2\cdot8 \\ V_B=\pi\cdot25\cdot8 \\ V_B=200\pi \end{gathered}`

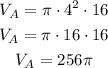
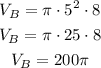
After pumping the water from container A to container B, the following amount remains in container A:

Remaining amount of water in A=256π-200π

Remaining amount of water in A=56π

Now, we obtain that the empty percentage that results in A is:

Empty percentage that results in A=200/256*100

Empty percentage that results in A=78.125%

Empty percentage that results in A≈78.1%