Okay, here we have this:
Considering the provided information, we are going to calculate what is the percent of Container A that is empty after the pumping is complete, so we obtain the following:
First we will calculate the volume of each cylinder using the following formula:
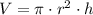
Applying:
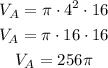
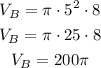
After pumping the water from container A to container B, the following amount remains in container A:
Remaining amount of water in A=256π-200π
Remaining amount of water in A=56π
Now, we obtain that the empty percentage that results in A is:
Empty percentage that results in A=200/256*100
Empty percentage that results in A=78.125%
Empty percentage that results in A≈78.1%