Question

A rocket is shot off from a launcher. The accompanying table represents the height of the rocket at given times, where x is time, in seconds, and y is height, in feet. Write a quadratic regression equation for this set of data, rounding all coefficients to the nearest tenth. Using this equation, find the height, to the nearest foot, at a time of 3.8 seconds.

Answer 1

Given

The data can be modeled using a quadratic regression equation.

Using the general form of a quadratic equation:

`y=ax^2\text{ + bx + c}`

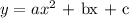
We should use a regression calculator to obtain the required coefficients. The graph of the equation is shown below:

The coefficients of the equation is:

`\begin{gathered} a\text{ = -17.5 (nearest tenth)} \\ b\text{ = }249.0\text{ (nearest tenth)} \\ c\text{ = }-0.5 \end{gathered}`

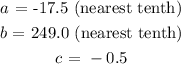
Hence, the regression equation is:

`y=-17.5x^2\text{ + 249.0x -0.5}`

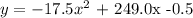
We can find the height (y) at a time of 3.8 seconds by substitution:

`\begin{gathered} y=-17.5(3.8)^2\text{ + 249}(3.8)\text{ - 0.5} \\ =\text{ }693 \end{gathered}`

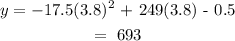
Hence, the height at time 3.8 seconds is 693 ft