Given
The data can be modeled using a quadratic regression equation.
Using the general form of a quadratic equation:
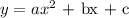
We should use a regression calculator to obtain the required coefficients. The graph of the equation is shown below:
The coefficients of the equation is:

Hence, the regression equation is:
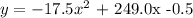
We can find the height (y) at a time of 3.8 seconds by substitution:
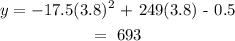
Hence, the height at time 3.8 seconds is 693 ft