Question

I'm blanking on how to do this, I learned it so long ago, any help would be greatly appreciated. More interested on how to do it than the answer.

Answer 1

`(16 y^(22))/(x^(10)z^(10))`

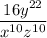
Explanation:

Given expression is ,

`\sf\longrightarrow \bigg((2x^3y^(-5)z^8)/(8x^(-2)y^6z^3)\bigg)^(-2)`

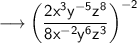
This would be simplified using the law of exponents , some of which I will use here are ,

• 
  `(an)^m = a^m n^m`
• 
  `(a^m)/(a^n)=a^(m-n)`

• 
  `a^m a^n = a^(m+n)`
• 
  `a^(-n) = (1)/(a^n)`

Using the above laws ,

`\sf \longrightarrow \bigg[ (2)/(8) \bigg((x^3)/(x^(-2))\bigg)\bigg((y^(-5))/(y^6)\bigg)\bigg((z^8)/(z^3)\bigg) \bigg]^(-2)`

Using the second law mentioned above , we have,

`\sf \longrightarrow \bigg[ (1)/(4)(x^(3+2))(y^(-5-6))(z^(8-3))\bigg]^(-2)`

Simplify ,

`\sf \longrightarrow \bigg[(1)/(4) x^5y^(-11)z^5\bigg]^(-2)`

Using the first law mentioned above , we have,

`\sf \longrightarrow \bigg[ (1)/(4^(-2)) x^(5(-2)) y^(-11(-2)) z^(5(-2))\bigg]`

Simplify,

`\sf \longrightarrow 4^2x^(-10)y^(22) z^(-10)`

Finally using the fourth law mentioned above , we have ,

`\sf \longrightarrow \boxed{\bf (16 y^(22))/(x^(10)z^(10))}`

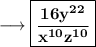
Option K is the correct answer.