The question provides the following parameters:
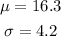
For 15 minutes, the z-score is calculated using the formula:
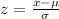
At x = 15:

The probability is calculated using the formula:
![P(X<15)=Pr(z<-0.3)=Pr(z<0)-Pr(0From tables, we have:[tex]\begin{gathered} Pr(z<0)=0.5 \\ Pr(0Therefore, the probability is given to be:[tex]\begin{gathered} P(X<15)=0.5-0.1179 \\ P(X<15)=0.38 \end{gathered}]()
The expected number of callers will be calculated using the formula:
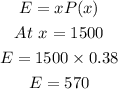
Therefore, the expected number of callers whose calls last less than 15 minutes is 570 callers.