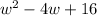Question

Perform the indicated operation. (w 3 + 64) ÷ (4 + w)

Answer 1

w³ + 64 = w³ + 4³ = (w+4)³ - 3*w*4(w+4) = (w+4)[(w+4)² - 12w]

(w³ + 64) ÷ (w+4)
=(w+4)[(w+4)² - 12w] ÷ (w+4)
= (w+4)² - 12w
= w² -4w + 16

Answer 2

The expression
`(\left(w^3+64\right))/(w+4)` becomes
`w^2-4w+16`

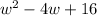
Explanation:

Given : Expression
`(\left(w^3+64\right))/(w+4)`

We have to find the simplified value of given expression.

Consider the given expression
`(\left(w^3+64\right))/(w+4)`

Rewrite 64 as
`4^3`

`=w^3+4^3`

`\mathrm{Apply\:Sum\:of\:Cubes\:Formula:\:}x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)`

`w^3+4^3=\left(w+4\right)\left(w^2-4w+4^2\right)`

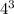
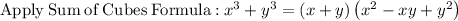
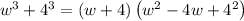
Simplify,

`=\left(w+4\right)\left(w^2-4w+4^2\right)`

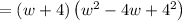
Given expression becomes,

`=(\left(w+4\right)\left(w^2-4w+16\right))/(w+4)`

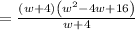
Cancel common factors, we have,

`=w^2-4w+16`

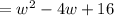
Thus, The expression
`(\left(w^3+64\right))/(w+4)` becomes
`w^2-4w+16`