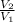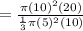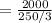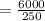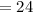Question

The radius of the base of a cylinder is 10 centimeters, and its height is 20 centimeters. A cone is used to fill the cylinder with water. The radius of the cone's base is 5 centimeters, and its height is 10 centimeters.

The number of times one needs to use the completely filled cone to completely fill the cylinder with water is.....

Answer 1

Im like 90% sure that your answer should be 2.

Answer 2

24 times.

Explanation:

Since, the volume of a cone,

`V=(1)/(3)\pi r^2 h`

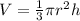
While, the volume of a cylinder,

`V=\pi r^2 h`

Where, r = radius,

h = height,

Thus, the volume of the cone having radius 5 cm and height 10 cm,

`V_1=(1)/(3)\pi (5)^2(10)`

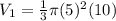
And, the volume of the cylinder having radius 10 cm, and 20 cm,

`V_2=\pi (10)^2 (20)`

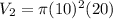
Hence, the number of times we need to use cone to completely fill the cylinder =
`(V_2)/(V_1)`

`=(\pi (10)^2 (20))/((1)/(3)\pi (5)^2(10))`

`=(2000)/(250/3)`

`=(6000)/(250)`

`=24`