For there to be a region bounded by the two parabolas, you first need to find some conditions on

. The two parabolas must intersect each other twice, so you need two solutions to
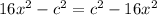
You have
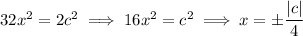
which means you only need to require that
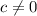
. With that, the area of any such bounded region would be given by the integral

since
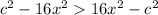
for all
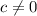
. Now,
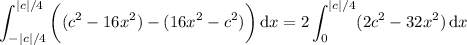
by symmetry across the y-axis. Integrating yields
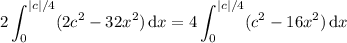
![=4\left[c^2x-\frac{16}3x^3\right]_(x=0)^(x=|c|/4)](https://img.qammunity.org/2018/formulas/mathematics/college/lbbv8rsahoezbbkw0q4rf724sgwzqucm55.png)

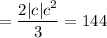
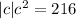
Since
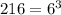
, you have

.