Answer:
1) 9/20
2) 5/11
Explanation:
For the first question: We read the number "0.45" as "45 hundredths," and we write it as the fraction 45/100. Of course, since 45 and 100 share the common factor 5, we can reduce this fraction by dividing the numerator and denominator by 5 to get the reduced form 9/20.
For our second problem, we need to perform a bit of "mathematical surgery" to find the appropriate fraction for x = 0.454545... First, the dots tell us that this fraction is repeating - those 45s will keep going on and on forever. When we multiply x by 100, then, we move the decimal two places to the right, but the repeating part still remains, giving us
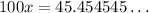
From here, we can "surgically remove" the repeating bit using our original value of x:
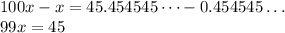
And from here, we just have to divide both sides of the equation by 99 to solve for x:
