Answer:
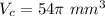
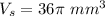
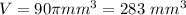
Explanation:
Given : A capsule consisting of a cylinder of radius 3 mm and height 6 mm with a hemisphere on each end of radius 3 mm.
To find : What is the volume of the item described?
Solution :
First we find the volume of the cylinder,
The volume of a cylinder is
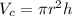
where,
r is the radius of the cylinder = 3 mm
h is the height of the cylinder = 6 mm
substitute the values
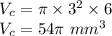
Secondly we find the volume of the two hemisphere,
The volume of the sphere is
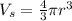
where,
r is the radius of the cylinder = 3 mm
substitute the values,
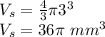
Thirdly we find the volume of the capsule,
The volume of the capsule = The volume of a cylinder + The volume of the two hemisphere
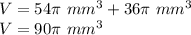
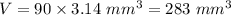
Therefore, Option 2,3 and 6 are correct.