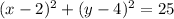Answer:
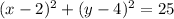
Explanation:
Since, the diameter of the circle having the end points (-2, 1) and (6, 7),
Thus, by the distance formula,

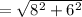
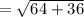

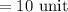
So, the radius of the circle =
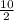 = 5 unit,
= 5 unit,
Let the equation of the circle is,
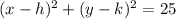
Where, (h, k) is the center of the circle,
Since, points (-2, 1) and (6, 7) are on the circle,
They must satisfy the equation of the circle,

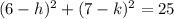
By solving these equations,
We get,
h = 2, k = 4
Hence, the equation of the circle would be,