Question

Select the correct trigonometric ratios for angle 0

Answer 1

A, D, and F

Explanation:

First off, we're not given the hypotenuse's length, so let's use the Pythagorean Theorem to find it:

`1^2+3^2=c^2\\1+9=c^2\\10=c^2\\c=√(10)`

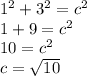
With that, we can refer to SOH-CAH-TOA to help us find sine, cosine, and tangent:

SOH (Sine = Opposite/Hypotenuse)

`sin(\theta)=1/√(10)=√(10)/10`

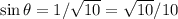
CAH (Cosine = Adjacent/Hypotenuse)

`cos(\theta)=3/√(10)=3√(10)/10`

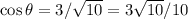
TOA (Tangent = Opposite/Adjacent)

`tan(\theta)=1/3`

From this, we can see that A matches up with sine, and we can eliminate B and C.

Cosecant, secant, and cotangent are all reciprocals of the three basic trig ratios:

`\csc{\theta}=1/sin(\theta)=√(10)\\\sec{\theta}=1/cos(\theta)=√(10)/3\\\cot{\theta}=1/tan(\theta)=3`

D matches with cosecant, and F matches with cotangent, so the correct trig rations for θ are A, D, and F.