Question

Example 3

L1 and 22 form a linear pair. If m_1 = 4 m22, find the measure of each of the two angles.

Answer 1

We conclude that

• The angle ∠1 = x = 36°

• The angle ∠2 = 4x = 4(36°) = 144°

Explanation:

Given

<1 and <2 form a linear pair

m∠1 = 4m∠2

To determine

Find the measure of each of the two angles.

Important Points about linear pair:

• We know that when two lines meet or intersect, we get a linear pair of angles.

• Linear pairs are basically two adjacent angles that form a line.

• The measure of two adjacent angles forming a straight line is 180, meaning they are supplementary.

As

<1 and <2 form a linear pair

m∠1 = 4m∠2

In other words, angle 1 is 4 times the measure of angle ∠2.

Let the angle ∠1 be = x

As the angle 1 is 4 times the measure of angle ∠2, so

The angle 2 will be = 4x

As <1 and <2 forms a linear pair, thus the measure of the sum of <1 and <2 will be 180°, so

`x + 4x = 180`

`5x = 180`

divide both sides by 5

`(5x)/(5)\:=\:(180)/(5)`

`\:x=36^(\circ )`

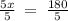
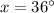
Thus, we conclude that

• The angle ∠1 = x = 36°

• The angle ∠2 = 4x = 4(36°) = 144°