Answer:
Using logarithmic rule:
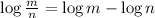
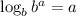
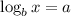 then
then
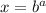
Given that,
Sound intensity of a typical vacuum cleaner = 80 dB
Sound intensity of burst of eardrum = 160 dB
Let, I₁ and I₂ b e the intensity of typical vacuum and intensity of eardrum.
Use the formula:
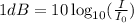
As per the statement
The sound intensity of a typical vacuum cleaner is 80 dB (decibels).
⇒
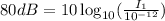
Divide both sides by 10 we have;
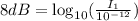
Apply the logarithmic rules:
then;
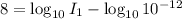
⇒
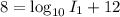
Subtract 12 from both sides we have;
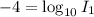
⇒
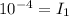 ......[A}
......[A}
It is also given that: Sound intensity of 160 dB will burst an eardrum.
⇒
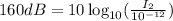
Divide both sides by 10 we have;
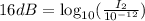
Apply the logarithmic rules:
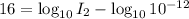
⇒
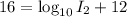
Subtract 12 from both sides we have;
⇒
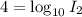
⇒
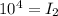 ......[B]
......[B]
We have to find how many times louder is the sound that will burst an eardrum than the sound of a vacuum cleaner.
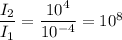
⇒
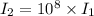
Therefore,
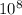 times louder is the sound that will burst an eardrum than the sound of a vacuum cleaner
times louder is the sound that will burst an eardrum than the sound of a vacuum cleaner