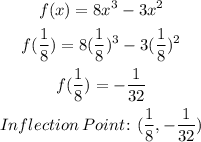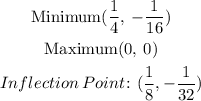
1) To find the relative maxima of a function, we need to perform the first derivative test. It tells us whether the function has a local maximum, minimum r neither.
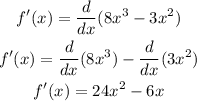
2) Let's find the points equating the first derivative to zero and solving it for x:
![\begin{gathered} 24x^2-6x=0 \\ x_{}=(-\left(-6\right)\pm\:6)/(2\cdot\:24),\Rightarrow x_1=(1)/(4),x_2=0 \\ f^(\prime)(x)>0 \\ 24x^2-6x>0 \\ (24x^2)/(6)-(6x)/(6)>(0)/(6) \\ 4x^2-x>0 \\ x\mleft(4x-1\mright)>0 \\ x<0\quad \mathrm{or}\quad \: x>(1)/(4) \\ f^(\prime)(x)<0 \\ 24x^2-6x<0 \\ 4x^2-x<0 \\ x\mleft(4x-1\mright)<0 \\ 0Now, we can write out the intervals, and combine them with the domain of this function since it is a polynomial one that has no discontinuities:[tex]\mathrm{Increasing}\colon-\infty\: <strong>3) </strong> Finally, we need to plug the x-values we've just found into the original function to get their corresponding y-values:[tex]\begin{gathered} f(x)=8x^3-3x^2 \\ f(0)=8(0)^3-3(0)^2 \\ f(0)=0 \\ \mathrm{Maximum}\mleft(0,0\mright) \\ x=(1)/(4) \\ f((1)/(4))=8\mleft((1)/(4)\mright)^3-3\mleft((1)/(4)\mright)^2 \\ \mathrm{Minimum}\mleft((1)/(4),-(1)/(16)\mright) \end{gathered}]()
4) Finally, for the inflection points. We need to perform the 2nd derivative test:
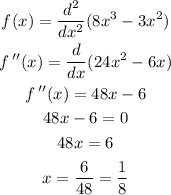
Now, let's plug this x value into the original function to get the y-corresponding value: