Question

One bag contains three white marbles and five black marbles, and a second bag contains four white marbles and six black marbles. A person draws one marble from each bag. Find the probability that both marbles are black.

Answer 1

5/8 the first bag and 3/5 for the second bag.

Answer 2

Answer:
`(3)/(8)`

Explanation:

Formula for probability :-

`\text{Probability}=\frac{\text{Favorable outcomes}}{\text{Total outcomes}}`

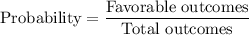
Given : One bag contains 3 white marbles and 5 black marbles, and a second bag contains 4 white marbles and 6 black marbles.

Probability of drawing a black marble from first bag
`P(B_1=)(5)/(5+3)=(5)/(8)`

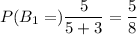
Probability of drawing a black marble from second bag
`P(B_2)=(6)/(6+4)=(6)/(10)`

Since the event of drawing marbles from each bag is independent, then

If a person draws one marble from each bag, then the probability that both marbles are black will be the product of both events :-

`P(B_1)* P(B_2)\\\\=(5)/(8)*(6)/(10)=(3)/(8)`

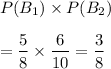
Hence, the required answer =
`(3)/(8)`