Question

Last year, Bob had $10,000 to invest. He invested some of it in an account that paid 10% simple interest per year, and he invested the rest in an account that paid 8% simple interest per year. After one year, he received a total of $820 in interest. How much did he invest in each account?

Answer 1

Given:

The total amount is P = $10,000.

The rate of interest is r(1) = 10% 0.10.

The other rate of interest is r(2) = 8%=0.08.

The number of years for both accounts is n = 1 year.

The total interest earned is A = $820.

The objective is to find the amount invested in each account.

Step-by-step explanation:

Consider the amount invested for r(1) as P(1), and the interest earned as A(1).

The equation for the amount obtained for r(1) can be calculated as,

`\begin{gathered} A_1=P_1* n* r_1 \\ A_1=P_1*1*0.1 \\ A_1=0.1P_1\text{ . . . . .(1)} \end{gathered}`

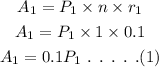
Consider the amount invested for r(2) as P(2), and the interest earned as A(2).

The equation for the amount obtained for r(2) can be calculated as,

`\begin{gathered} A_2=P_2* n* r_2 \\ A_2=P_2*1*0.08 \\ A_2=0.08P_2\text{ . . . . . (2)} \end{gathered}`

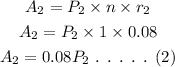
Since, it is given that the total interest earned is A=$820. Then, it can be represented as,

`A=A_1+A_2\text{ . . . . . (3)}`

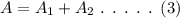
On plugging the obtained values in equation (3),

`820=0.1P_1+0.08P_2\text{ . . . . .(4)}`

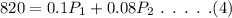
Also, it is given that the total amount is P = $10,000. Then, it can be represented as,

`\begin{gathered} P=P_1+P_2 \\ 10000=P_1+P_2 \\ P_1=10000-P_2\text{ . }\ldots\ldots.\text{. .(3)} \end{gathered}`

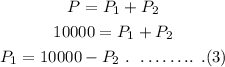
Substitute the equation (3) in equation (4).