Question

The heights, in feet, of 12 trees in a park are shown below.8, 11, 14, 16, 17, 21, 21, 24, 27, 31, 43, 47Use the drop-down menus to explain the interquartile range of the data.

Answer 1

Given:

The heights, in feet, of 12 trees in a park are:

8,11,14,16,17,21,21,24,27,31,43,47.

Required:

To find the interquartile range of the given data.

Step-by-step explanation:

We have given the heights of 12 trees in feet.

Therefore, the total number of quantitties (elements) in given data is even.

Thus, the median (M) of the data is,

`\begin{gathered} M=(21+21)/(2) \\ \Rightarrow M=(42)/(2) \\ \Rightarrow M=21 \end{gathered}`

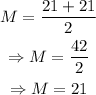
The median (Q) of the first half of the data 8,11,14,16,17 is given by,

`Q=14`

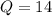
since the number of quantities are odd.

The median (Q') of the second half of the data 24,27,31,43,47 is given by,

`Q^(\prime)=31`

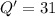
since the number of quantities are odd.

Hence, the interqurtile range (R) is,

`\begin{gathered} R=Q^(\prime)-Q \\ \Rightarrow R=31-14 \\ \Rightarrow R=17 \end{gathered}`

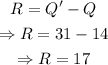
Final Answer:

The interquartile range is,

`R=17`

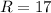
The first option is spread.

The second option is range.

The third option is 17.

The fourth option is middle 50%.