Given:
The heights, in feet, of 12 trees in a park are:
8,11,14,16,17,21,21,24,27,31,43,47.
Required:
To find the interquartile range of the given data.
Step-by-step explanation:
We have given the heights of 12 trees in feet.
Therefore, the total number of quantitties (elements) in given data is even.
Thus, the median (M) of the data is,
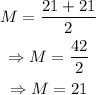
The median (Q) of the first half of the data 8,11,14,16,17 is given by,
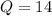
since the number of quantities are odd.
The median (Q') of the second half of the data 24,27,31,43,47 is given by,
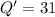
since the number of quantities are odd.
Hence, the interqurtile range (R) is,
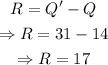
Final Answer:
The interquartile range is,
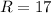
The first option is spread.
The second option is range.
The third option is 17.
The fourth option is middle 50%.