Question

A 1500 kg car traveling at 10 m/s suddenly runs out of gaswhile approaching the valley shown in FIGURE EX10.11. The alertdriver immediately puts the car in neutral so that it will roll.What will be the car’s speed as it coasts into the gas station onthe other side of the valley?

Answer 1

If the car does not brake, its mechanical energy will be conserved along all its trajectory.

Then, the sum of the kinetic energy (K) of the car and its gravitational potential energy (U) will be the same for any two points in the trajectory:

`K_1+U_1=K_2+U_2`

The kinetic energy of an object with mass m and speed v is:

`K=(1)/(2)mv^2`

The gravitational potential energy of an object with mass m at a height h above a reference level, is:

`U=mgh`

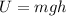
Where g is the acceleration of gravity.

In the beginning, the car has a height of 10m and a speed of 10m/s. In the end, the car reaches the gas station at a height 15m and a unknown speed v.

Then, the initial speed and height are known, as well as the final height. Use the equation for the conservation of mechanical energy to isolate v_2, the unknown final speed of the car:

`\begin{gathered} K_2+U_2=K_1+U_1 \\ \Rightarrow(1)/(2)mv_2^2+mgh_2=(1)/(2)mv_1^2+mgh_1 \\ \Rightarrow(1)/(2)v_2^2+gh_2=(1)/(2)v_1^2+gh_1 \\ \Rightarrow(1)/(2)v_2^2=(1)/(2)v_1^2+gh_1-gh_2 \\ \Rightarrow(1)/(2)v_2^2=(1)/(2)v_1^2+g\mleft(h_1-h_2\mright) \\ \Rightarrow v_2^2=v_1^2+2g\mleft(h_1-h_2\mright) \\ \\ \therefore v_2=√(v_1^2+2g(h_1-h_2)) \end{gathered}`

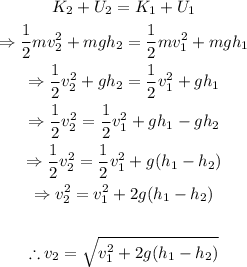
Replace v_1=10m/s, h_1=10m, h_2=15m and g=9.8m/s^2 to find the speed of the car as it reaches the gas station:

`\begin{gathered} v_2=\sqrt{(10(m)/(s))^2+2(9.8(m)/(s^2))(10m-15m)} \\ =1.4142...(m)/(s) \\ \approx1.4(m)/(s) \end{gathered}`

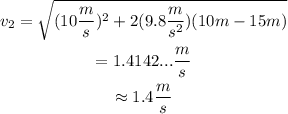
Therefore, the car's speed as it coasts into the gas station on the other side of the valley will be approximately 1.4 meters per second.