Question

The sum or product of a non-zero rational number and an irrational number is always

1.Rational.
2.Irrational.
3.A repeating decimal.
4.A fraction.

Answer 1

the product of a non-zero rational and an irrational number is always irrational (2)

Answer 2

Option 2 - Irrational

Explanation:

To find : The sum or product of a non-zero rational number and an irrational number is always

Solution :

By the statement,

→ "The sum of a rational number and an irrational number is irrational."

Example : Let a rational number 3 and irrational number
`√(5)`

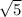
Sum of rational and irrational number

`3+√(5)= 3+2.236067977.....=5.236067977....`

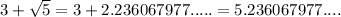
5.236067977.... is a irrational number as if you add a non-repeating and non-terminating decimal to a repeating decimal, you will have a repeating decimal.

→ "The product of a non-zero rational number and an irrational number is irrational."

Example : Let a rational number 3 and irrational number
`√(5)`

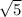
Sum of rational and irrational number

`3*√(5)= 3*2.236067977.....=6.708203931.....`

6.708203931...... is a irrational number as If you multiply any irrational number by the rational number it gives you irrational except zero which is rational.

Therefore, Option 2 is correct.

The sum or product of a non-zero rational number and an irrational number is always irrational.